Primzahlen
einfacher Primzahlentest
Bisher gibt es noch keine Möglichkeit, mit Hilfe einer Rechenvorschrift eine Primzahl einfach so zu bestimmen. Braucht man eine zufällige Primzahl zwischen 2 und einer Obergrenze, muss man eine zufällige Zahl bestimmen und dann testen, ob es eine Primzahl ist. Fällt der Test negativ aus, muss man eine neue Zufallszahl bestimmen und den Test erneut ausführen.
Prinzip: Eine Primzahl ist eine Zahl größer als 1, die nur durch 1 und sich selber teilbar ist. Es muss also nur geprüft werden, ob ein Primzahlenkandidat durch eine Zahl ohne Rest teilbar ist. Wenn das der Fall ist, ist er durchgefallen :-(.
Als erstes testet man auf 2 als Teiler. Liefert die Modulo-Funktion eine 0 (also durch 2 geteilt und keinen Rest), ist die Zahl gerade. Dann wird einfach 1 addiert und die Zahl ist ungerade. Damit fällt im folgenden Test die 2 als Teiler raus und es kann mit der 3 begonnen werden.
Wie weit muss man testen? Es soll am Beispiel der 18 gezeigt werden. Es wird immer 18 durch den Teiler geteilt und das ganzzahlige Ergebnis sowie der Rest der ganzzahligen Division betrachtet. Wem das Verfahren irgendwie bekann vorkommt, erinnert sich sicher gerade an die ersten Teilerübungen in der Grundschule.
| Teiler | Ergebnis | Rest |
|---|---|---|
| 3 | 6 | 0 |
| 4 | 4 | 2 |
| 5 | 3 | 3 |
| 6 | 3 | 0 |
| 7 | 2 | 4 |
| 8 | 2 | 2 |
| 9 | 2 | 0 |
| 10 | 1 | 8 |
| 11 | 1 | 7 |
Ab der 10 geht es immer so weiter. Das Ergebnis ist 1 und der Rest nähert sich der 18.
Das heißt aber, dass man eigentlich nur die 3, die 4 und die 5 prüfen muss. Denn die 6 kann wegfallen, da bei der Division durch 6 die 3 ohne Rest das Ergebnis ist. Die 3
ist aber schon geprüft worden.
- Der Primzahlentest muss nur bist zur aufgerundeten Wurzel aus der Testzahl gemacht werden.
- Liefert eine Modulo-Funktion als Ergebnis 0, kann Zählschleife abgebrochen werden.
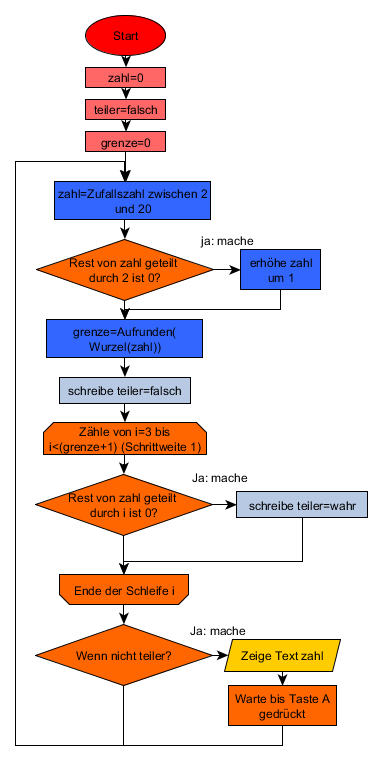
Aufgabe: Die letzte Regel ist im Programmablaufplan noch nicht implementiert. Ändere das bitte noch.
größere Primzahlen
Für die Ausgabe von größen Primzahlen ist der kleine Calliope-Bildschirm ungeignet. Deshalb erfolgt jetzt die Ausgabe über den seriellen Monitor. Gleichzeitig wird noch die Zeit gemessen, die zur Berechnung einer Primzahl vergeht. das Bild zeigt einen Ausschnitt aus dem seriellen Monitor, wenn Primzahlen bis zu einer Million berechnet werden.
Aufgabe: Eine schnellere Berechnung ist durch eine weitere Verbesserung des Programms möglich. Da nur ungerade Zahlen geprüft werden, kann die Division durch eine gerade Zahl nie ohne Rest erfolgen. Damit kann der Test mit allen geraden Zahlen entfallen. Die Zählschleife beginnt mit 3 und zählt in Einerschritten hoch. Zählt man in Zweierschritten hoch, fallen alle geraden Zahlen als Teiler weg. Überpr?fe die dadurch erreichte Zeitersparnis!
Bis zur Million ist es noch im Zeitrahmen. Gehen die Zufallszahlen bis zu 10 Millionen, kann es schon Mal mehr als eine Minute dauern. Fazit: der Calliope mini ist zur Berechnung von großen Primzahlen ungeeignet!
Hinweis: Wer den berechneten Zahlen nicht traut, kann sie im Primzahlentest prüfen.


einfacher Primzahlentest
Bisher gibt es noch keine Möglichkeit, mit Hilfe einer Rechenvorschrift eine Primzahl einfach so zu bestimmen. Braucht man eine zufällige Primzahl zwischen 2 und einer Obergrenze, muss man eine zufällige Zahl bestimmen und dann testen, ob es eine Primzahl ist. Fällt der Test negativ aus, muss man eine neue Zufallszahl bestimmen und den Test erneut ausführen.
Prinzip: Eine Primzahl ist eine Zahl größer als 1, die nur durch 1 und sich selber teilbar ist. Es muss also nur geprüft werden, ob ein Primzahlenkandidat durch eine Zahl ohne Rest teilbar ist. Wenn das der Fall ist, ist er durchgefallen :-(.
Als erstes testet man auf 2 als Teiler. Liefert die Modulo-Funktion eine 0 (also durch 2 geteilt und keinen Rest), ist die Zahl gerade. Dann wird einfach 1 addiert und die Zahl ist ungerade. Damit fällt im folgenden Test die 2 als Teiler raus und es kann mit der 3 begonnen werden.

Wie weit muss man testen? Es soll am Beispiel der 18 gezeigt werden. Es wird immer 18 durch den Teiler geteilt und das ganzzahlige Ergebnis sowie der Rest der ganzzahligen Division betrachtet. Wem das Verfahren irgendwie bekann vorkommt, erinnert sich sicher gerade an die ersten Teilerübungen in der Grundschule.
| Teiler | Ergebnis | Rest |
|---|---|---|
| 3 | 6 | 0 |
| 4 | 4 | 2 |
| 5 | 3 | 3 |
| 6 | 3 | 0 |
| 7 | 2 | 4 |
| 8 | 2 | 2 |
| 9 | 2 | 0 |
| 10 | 1 | 8 |
| 11 | 1 | 7 |
Ab der 10 geht es immer so weiter. Das Ergebnis ist 1 und der Rest nähert sich der 18.
Das heißt aber, dass man eigentlich nur die 3, die 4 und die 5 prüfen muss. Denn die 6 kann wegfallen, da bei der Division durch 6 die 3 ohne Rest das Ergebnis ist. Die 3
ist aber schon geprüft worden.
- Der Primzahlentest muss nur bist zur aufgerundeten Wurzel aus der Testzahl gemacht werden.
- Liefert eine Modulo-Funktion als Ergebnis 0, kann Zählschleife abgebrochen werden.
Aufgabe: Die letzte Regel ist im Programmablaufplan noch nicht implementiert. Ändere das bitte noch.
größere Primzahlen
Für die Ausgabe von größen Primzahlen ist der kleine Calliope-Bildschirm ungeignet. Deshalb erfolgt jetzt die Ausgabe über den seriellen Monitor. Gleichzeitig wird noch die Zeit gemessen, die zur Berechnung einer Primzahl vergeht. das Bild zeigt einen Ausschnitt aus dem seriellen Monitor, wenn Primzahlen bis zu einer Million berechnet werden.


Aufgabe: Eine schnellere Berechnung ist durch eine weitere Verbesserung des Programms möglich. Da nur ungerade Zahlen geprüft werden, kann die Division durch eine gerade Zahl nie ohne Rest erfolgen. Damit kann der Test mit allen geraden Zahlen entfallen. Die Zählschleife beginnt mit 3 und zählt in Einerschritten hoch. Zählt man in Zweierschritten hoch, fallen alle geraden Zahlen als Teiler weg. Überprüfe die dadurch erreichte Zeitersparnis!
Bis zu 10 Million ist es noch im Zeitrahmen. Gehen die Zufallszahlen bis zu 100 Millionen, kann es schon Mal mehr als eine Minute dauern. Fazit: der Calliope mini ist zur Berechnung von großen Primzahlen ungeeignet! ABER: Das von MakeCode generierte Programm ist deutlich schneller als das OpenRoberta-Programm.
Hinweis: Wer den berechneten Zahlen nicht traut, kann sie im Primzahlentest prüfen.
Mit dem OLED-Display SSD 1306 kann man sich große Zahlen und die Laufzeit des Programms auch direkt anzeigen lassen.
Die maximale Zahl, die beim Würfeln eingegeben werden kann, ist 1 073 741 824. Das entspricht 230-1. Bei größeren Zahlen kommen keine vernünftigen Ergebnisse heraus, da der Zahlenbereich des Calliope mini überschritten wird.

einfacher Primzahlentest
Bisher gibt es noch keine Möglichkeit, mit Hilfe einer Rechenvorschrift eine Primzahl einfach so zu bestimmen. Braucht man eine zufällige Primzahl zwischen 2 und einer Obergrenze, muss man eine zufällige Zahl bestimmen und dann testen, ob es eine Primzahl ist. Fällt der Test negativ aus, muss man eine neue Zufallszahl bestimmen und den Test erneut ausführen.
Prinzip: Eine Primzahl ist eine Zahl größer als 1, die nur durch 1 und sich selber teilbar ist. Es muss also nur geprüft werden, ob ein Primzahlenkandidat durch eine Zahl ohne Rest teilbar ist. Wenn das der Fall ist, ist er durchgefallen :-(.
Als erstes testet man auf 2 als Teiler. Liefert die Modulo-Funktion eine 0 (also durch 2 geteilt und keinen Rest), ist die Zahl gerade. Dann wird einfach 1 addiert und die Zahl ist ungerade. Damit fällt im folgenden Test die 2 als Teiler raus und es kann mit der 3 begonnen werden.
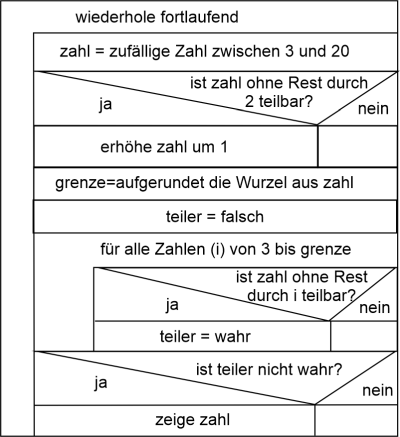
Wie weit muss man testen? Es soll am Beispiel der 18 gezeigt werden. Es wird immer 18 durch den Teiler geteilt und das ganzzahlige Ergebnis sowie der Rest der ganzzahligen Division betrachtet. Wem das Verfahren irgendwie bekann vorkommt, erinnert sich sicher gerade an die ersten Teilerübungen in der Grundschule.
| Teiler | Ergebnis | Rest |
|---|---|---|
| 3 | 6 | 0 |
| 4 | 4 | 2 |
| 5 | 3 | 3 |
| 6 | 3 | 0 |
| 7 | 2 | 4 |
| 8 | 2 | 2 |
| 9 | 2 | 0 |
| 10 | 1 | 8 |
| 11 | 1 | 7 |
Ab der 10 geht es immer so weiter. Das Ergebnis ist 1 und der Rest nähert sich der 18.
Das heißt aber, dass man eigentlich nur die 3, die 4 und die 5 prüfen muss. Denn die 6 kann wegfallen, da bei der Division durch 6 die 3 ohne Rest das Ergebnis ist. Die 3
ist aber schon geprüft worden.
- Der Primzahlentest muss nur bist zur aufgerundeten Wurzel aus der Testzahl gemacht werden.
- Liefert eine Modulo-Funktion als Ergebnis 0, kann Zählschleife abgebrochen werden.
Aufgabe: Die letzte Regel ist im Programmablaufplan noch nicht implementiert. Ändere das bitte noch.
größere Primzahlen
Für die Ausgabe von größen Primzahlen ist der kleine Calliope-Bildschirm ungeignet. Deshalb erfolgt jetzt die Ausgabe über den seriellen Monitor. Gleichzeitig wird noch die Zeit gemessen, die zur Berechnung einer Primzahl vergeht. das Bild zeigt einen Ausschnitt aus dem seriellen Monitor, wenn Primzahlen bis zu einer Million berechnet werden.

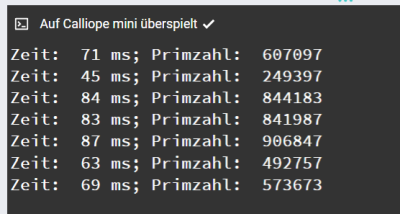
Aufgabe: Eine schnellere Berechnung ist durch eine weitere Verbesserung des Programms möglich. Da nur ungerade Zahlen geprüft werden, kann die Division durch eine gerade Zahl nie ohne Rest erfolgen. Damit kann der Test mit allen geraden Zahlen entfallen. Die Zählschleife beginnt mit 3 und zählt in Einerschritten hoch. Zählt man in Zweierschritten hoch, fallen alle geraden Zahlen als Teiler weg. Überprüfe die dadurch erreichte Zeitersparnis!
Leider kann als Obergrenze "nur" 2 Mrd. eingetragen werden. Bei größeren Zahlen verweigert das Programm den Dienst. Und dann dauert es auch schon mal einige Sekunden, bis die nächste Zahl angezeigt wird.
Fazit: der Calliope mini ist zur Berechnung von sehr großen Primzahlen ungeeignet! ABER: Das von Python generierte Programm ist deutlich schneller als das MakeCode-Programm.
Hinweis: Wer den berechneten Zahlen nicht traut, kann sie im Primzahlentest prüfen.

 Campus
Campus  Make Code
Make Code  Open Roberta Lab
Open Roberta Lab  Python
Python 