Make Code 
Open Roberta Lab 
Python 
Die kleinste Zelle aller Computer: die NAND-Schaltung
Unsere heutigen Computer sind aus Milliarden von Schaltern aufgebaut. Als Schalter verwendet man kein mechanisches Element, sondern den Transistor. Mit wenigen Transistoren lässt sich die kleinste Zelle aller Computer realisieren: die NAND-Schaltung. Aus der geschickten Verknüpfung vieler solcher NAND-Schaltungen lassen sich alle notwendigen Strukturen eines Mikroprozessors aufbauen.
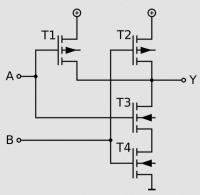
Die NAND-Schaltung (NICHT UND) hat zwei oder mehr Eingänge und einen Ausgang. Für zwei Eingänge sehen die Wahrheitstabelle und das Schaltbild so aus:
| A | B | Y |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
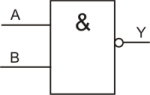
Schaltbild
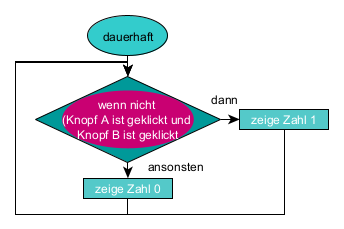
Eine einfache NAND-Schaltung lässt sich mit dem Calliope mini recht einfach realisieren.
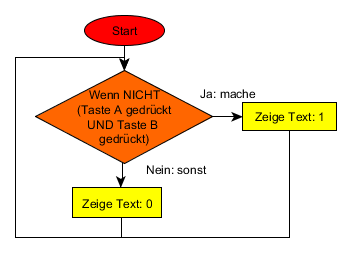
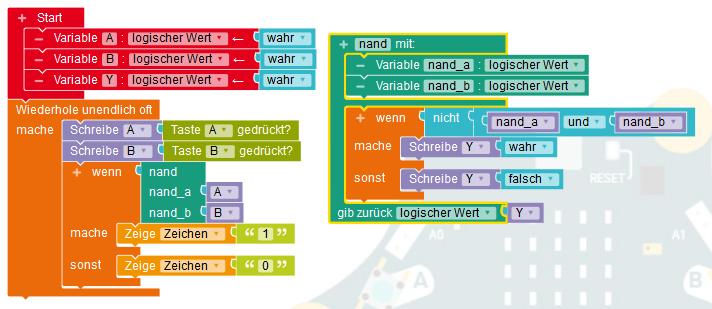
Nun braucht man aber für komplexe logische Schaltungen mehrere NAND-Verknüpfungen. Deshalb wird eine NAND-Funktion geschrieben, der man die beiden Werte A und B übergibt und die entsprechend der Wahrheitstabelle den Y-Wert zurückliefert.
Dieses Programm liefert die gleichen Ergebnisse wie das vorherige Programm, sieht aber wesentlich komplizierter aus. Warum der Aufwand?
Das sieht man in der nächsten Übung!
Unsere heutigen Computer sind aus Milliarden von Schaltern aufgebaut. Als Schalter verwendet man kein mechanisches Element, sondern den Transistor. Mit wenigen Transistoren lässt sich die kleinste Zelle aller Computer realisieren: die NAND-Schaltung. Aus der geschickten Verknüpfung vieler solcher NAND-Schaltungen lassen sich alle notwendigen Strukturen eines Mikroprozessors aufbauen.
Die NAND-Schaltung (NICHT UND) hat zwei oder mehr Eingänge und einen Ausgang. Für zwei Eingänge sehen die Wahrheitstabelle und das Schaltbild so aus:
| A | B | Y |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
Schaltbild
Eine einfache NAND-Schaltung lässt sich mit dem Calliope mini recht einfach realisieren.
Nun braucht man aber für komplexe logische Schaltungen mehrere NAND-Verknüpfungen. Deshalb wird eine NAND-Funktion geschrieben, der man die beiden Werte A und B übergibt und die entsprechend der Wahrheitstabelle den Y-Wert zurückliefert.
Dieses Programm liefert die gleichen Ergebnisse wie das vorherige Programm, sieht aber wesentlich komplizierter aus. Warum der Aufwand?
Das sieht man in der nächsten Übung!
