logische Grundschaltungen
Für die NOT-Funktion werden die beiden Anschlüsse des NAND zusammengelegt. Am Ausgang Y steht immer das negierte Signal von A zur Verfügung.
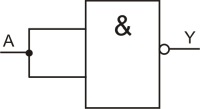
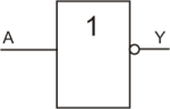
Schaltzeichen der NOT-Schaltung
Die NAND-Funktion im OpenRobertaLab wird zusammengefaltet.
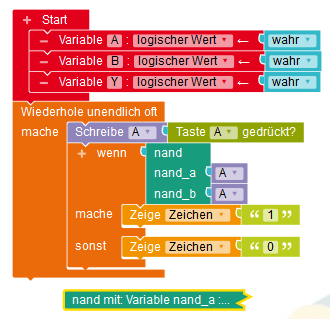
Die AND-Funktion wird durch eine NAND-Funktion mit nachfolgender Negation realisiert. Wenn alles richtig programmiert wurde, erhält man die folgende Wahrheitstabelle:
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
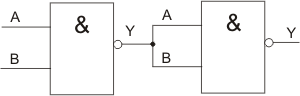
AND-Schaltung aus NANG-Gattern
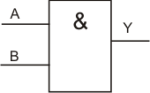
Schaltzeichen der AND-Schaltung
Die OR-Funktion negiert die beiden Eingänge und verknüpft die beiden Ausgänge der Negatoren über eine NAND-Schaltung. Wenn alles richtig programmiert wurde, erhält man die folgende Wahrheitstabelle:
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
Damit wird die NAND-Funktion insgesamt drei Mal aufgerufen.
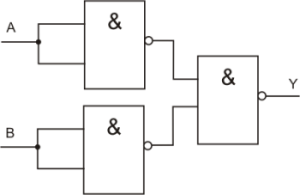
OR-Schaltung aus NANG-Gattern
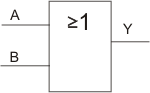
Schaltzeichen der OR-Schaltung
Die OR-Funktion arbeitet nicht wirklich gut: Der Ausgang Y soll 1 sein, wenn A oder B 1 sind. Im letzten Fall der Wahrheitstabelle sind beide Eingänge 1. Dann sollte die Funktion aber wieder eine 0 liefern.
Das Schaltbild realisiert die XOR-Funktion. Sie lässt sich mit der NAND-Funktion im Calliope mini nachbauen. Dabei sollte man beim Zusammenstellen der Blöcke von rechts im Schaltbild anfangen.
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
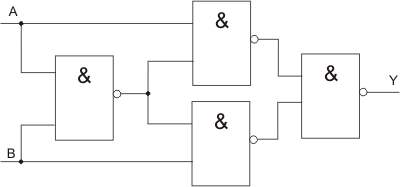
Schaltbild
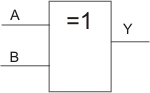
Schaltzeichen der XOR-Schaltung
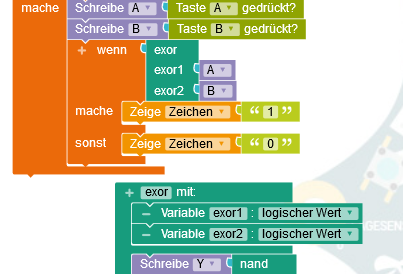
Da die XOR-Funktion im folgenden Schritt mehrmals benötigt wird, legt man sie wieder in eine Funktion. Das eigentliche Hauptprogramm ruft diese Funktion mit den beiden Eingabewerten A und B auf und die Funktion liefert das entsprechende Ergebnis zurück.
Die XOR-Funktion ruft also vier mal die NAND-Funktion auf, die wiederum die übergebenen Werte verknüpft. Wenn die Funktionen ordentlich funktionieren, können sie zusammengefaltet werden (mit rechts anklicken: Block zusammenfalten). Dann liegen die Funktionen nur noch als grüner Balken da und machen das Programm spürbar übersichtlicher.
Im nächsten Schritt wird mit der XOR-Funktion addiert.
Für die NOT-Funktion werden die beiden Anschlüsse des NAND zusammengelegt. Am Ausgang Y steht immer das negierte Signal von A zur Verfügung.


Schaltzeichen der NOT-Schaltung
Die NAND-Funktion wird zusammengefaltet.
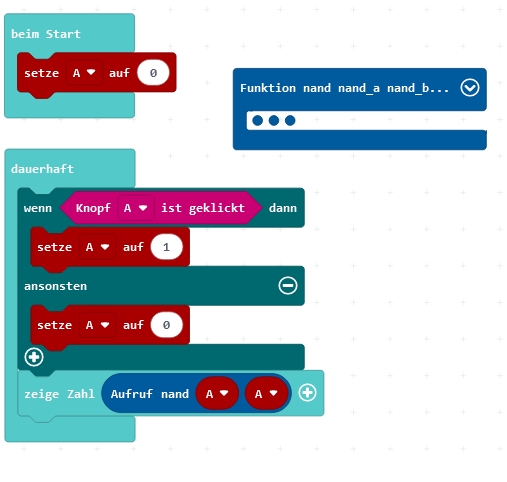
Die AND-Funktion wird durch eine NAND-Funktion mit nachfolgender Negation realisiert. Wenn alles richtig programmiert wurde, erhält man die folgende Wahrheitstabelle:
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
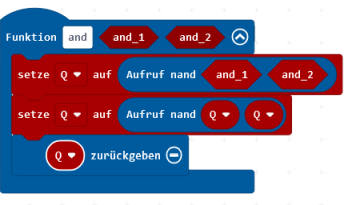

AND-Schaltung aus NAND-Gattern

Schaltzeichen der AND-Schaltung
Die OR-Funktion negiert die beiden Eingänge und verknüpft die beiden Ausgänge der Negatoren über eine NAND-Schaltung. Wenn alles richtig programmiert wurde, erhält man die folgende Wahrheitstabelle:
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
Im Programm wird die NAND-Funktion aufgerufen und ihr die beiden Ergebnisse der negierenden NAND-Funktionen übergenen.
Damit wird die NAND-Funktion insgesamt drei Mal aufgerufen.


OR-Schaltung aus NANG-Gattern

Schaltzeichen der OR-Schaltung
Die OR-Funktion wird durch eine nachfolgende Negation durch einen weiteren Aufruf einer NAND-Funktion zur NOR-Funktion. Da diese Funktion in einer folgenden Aufgabe für das RS-Flip-Flop benötigt wird, werden die Programmteile in einer extra Funktion mit dem Namen nor abgelegt. Als Ergebnis wird nur dann eine 1 angezeigt, wenn A und B 0 sind. In allen anderen Fällen erscheint eine 0. Überprüfen!
Die OR-Funktion arbeitet nicht wirklich gut: Der Ausgang Y soll 1 sein, wenn A oder B 1 sind. Im letzten Fall der Wahrheitstabelle sind beide Eingänge 1. Dann sollte die Funktion aber wieder eine 0 liefern.
Das Schaltbild realisiert die XOR-Funktion. Sie lässt sich mit der NAND-Funktion im Calliope mini nachbauen. Dabei sollte man beim Zusammenstellen der Blöcke von rechts im Schaltbild anfangen.
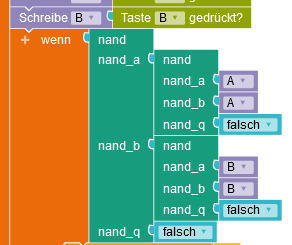
Hinweis: Obwohl nur 4 NAND-Schaltungen enthalten sind, wird die NAND-Funktion 5 Mal aufgerufen. Die Verknüpfung für das mittlere, obere NAND sieht so aus:

| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |

Schaltbild

Schaltzeichen der XOR-Schaltung
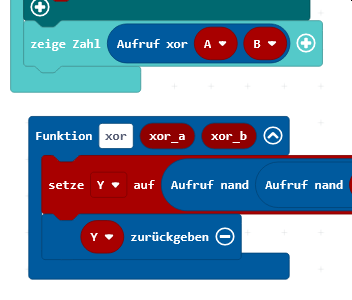
Da die XOR-Funktion im folgenden Schritt mehrmals benötigt wird, legt man sie wieder in eine Funktion. Das eigentliche Hauptprogramm ruft diese Funktion mit den beiden Eingabewerten A und B auf und die Funktion liefert das entsprechende Ergebnis zurück.
Die XOR-Funktion ruft also vier mal die NAND-Funktion auf, die wiederum die übergebenen Werte verknüpft. Wenn die Funktionen ordentlich funktionieren, können sie zusammengefaltet werden (mit rechts anklicken: Block verbergen). Dann liegen die Funktionen nur noch als blauer Balken da und machen das Programm spürbar übersichtlicher.

 Campus
Campus  Make Code
Make Code  Open Roberta Lab
Open Roberta Lab  Python
Python 