Wurzel ziehen
Wurzel aus Quadratzahlen
Das Halbierungsverfahren kann für verschiedene mathematischen Probleme verwendet werden. Hier wird es für das Ziehen einer Wurzel aus einer beliebigen Zahl benutzt.
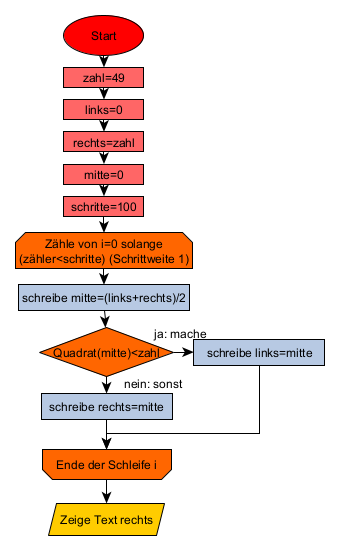
Es soll am Ziehen der Wurzel aus 49 beschrieben werden. Wir wissen, dass das Ergebnis 7 ist. Nur der Calliope mini weiß das nicht und muss deshalb die Wurzel berechnen.
- Es werden zwei Zahlen bestimmt, zwischen denen das Ergebnis auf jeden Fall liegt. Das sind in diesem Fall die beiden Zahlen 0 und 49. Die 0 nennen wir linke Grenze (links) und die 49 rechte Grenze (rechts).
- Es wird die Mitte zwischen diesen beiden Zahl berechnet: mitte=(links+rechts)/2. In diesem Fall ist das 24,5
- Von dem Wert mitte wird das Quadrat berechnet. 24,5² = 600,25
- Jetzt vergleicht man den Wert 600,25 mit der Zahl, aus der die Wurzel gezogen werden soll, also mit 49. 600,25 ist deutlich größer als 49. Denach ist 24,5 als Wurzel zu groß. Die gesuchte Wurzel muss kleiner sein, liegt also zwischen 0 und 24,5.
- Die rechte Grenze wird nun zu 24,5 geändert.
- Die nächste Berechnung geht bei Nummer 2 weiter.
Die Schritte 2-6 müssen nun oft genug durchgeführt werden. Das ist aber für den Calliope mini kein Problem: man nutzt einfach eine Zählschleife.
Im konkreten Fall wird die Berechnung 100 Mal durchgeführt. Am Ende wird die rechte Grenze ausgegeben: es erscheint die Zahl 7. Prima.
Setzt man die Schrittanzahl auf z.B. 10, wird die Berechnung zu zeitig abgebrochen und die ausgegebene Wurzel ist etwas größer als 7.
Die Idee für den ersten Teil stammt aus der Zeitschrift c’t, Ausgabe 12/2022, Seite 156 ff.
kontrollierter Abbruch
Wie oft muss nun aber die Schleife mindestens durchlaufen werden, damit die exakte Wurzel berechnet wird. An Stelle des geschätzten 100-fachen Durchlaufes wird die Schleife durch eine kontrollierte Abbruchbedingung nur sooft durchlaufen, wie es wirklich notwendig ist. Nach jeder Schleife wird ein Zähler um eins erhöht und zum Schluss nach der Ausgabe der Wurzel angezeigt. Im konkreten Fall sind das 55 Durchläufe!
Es zeigt sich auch, dass bei deutlich größeren Zahlen die Anzahl der Rechenschleifen nicht wesentlich steigt.

Wurzel aus jeder Zahl
Wieviel Schleifendurchläufe braucht man nun aber, um die Wurzel aus einer Zahl zu bestimmen, die keine Quadratzahl ist. Eigentlich solange, bis der rechte Wert mit dem linken Wert übereinstimmen. So einfach geht das aber nicht.
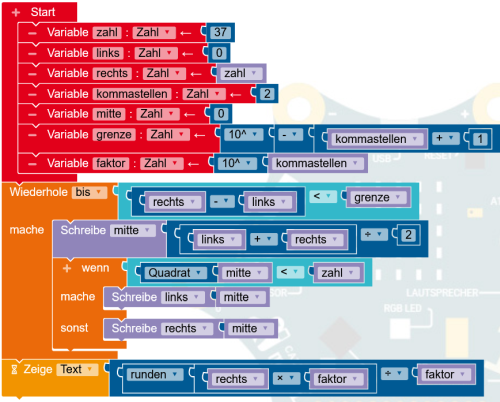
Wie groß ist z.B. die Wurzel aus 37? Aus 36 ist sie eindeutig 6. Die Wurzel aus 37 ist eine irrationale Zahl. Das heiß vereinfacht: sie hat eine unendliche große Menge an Kommastellen. Deshalb kann man nicht solange rechnen, bist rechts und links gleich sind. Das sind sie nie! Es gibt keine Zahl, die quadriert genau 37 ergibt.
Deshalb muss man bereits vor der Berechnung wissen, auf wieviel Nachkommastellen die Wurzel berechnet werden soll. Es muss einen kontrollierten Abbruch der Schleife geben.
Die Wurzel aus 37 soll mit zwei Kommastellen ausgegeben werden. Dazu wird die Differenz der beiden Werte rechts und links mit einer Grenze verglichen. Die Grenze wird aus der Anzahl der Kommastellen berechnet und ist hier 0,001. Die beiden Werte sind also nicht gleich, sondern unterscheiden sich um 0,001.
Nach der Berechnung wird die Wurzel aus dem Wert rechts mit den gewünschten Kommastellen angezeigt.
Wurzel aus Quadratzahlen
Das Halbierungsverfahren kann für verschiedene mathematischen Probleme verwendet werden. Hier wird es für das Ziehen einer Wurzel aus einer beliebigen Zahl benutzt.
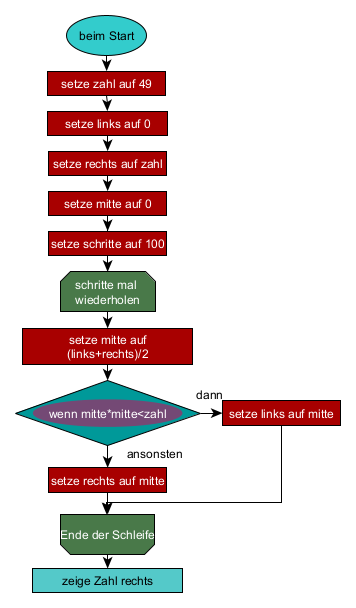
Es soll am Ziehen der Wurzel aus 49 beschrieben werden. Wir wissen, dass das Ergebnis 7 ist. Nur der Calliope mini weiß das nicht und muss deshalb die Wurzel berechnen.
- Es werden zwei Zahlen bestimmt, zwischen denen das Ergebnis auf jeden Fall liegt. Das sind in diesem Fall die beiden Zahlen 0 und 49. Die 0 nennen wir linke Grenze (links) und die 49 rechte Grenze (rechts).
- Es wird die Mitte zwischen diesen beiden Zahl berechnet: mitte=(links+rechts)/2. In diesem Fall ist das 24,5
- Von dem Wert mitte wird das Quadrat berechnet. 24,5² = 600,25
- Jetzt vergleicht man den Wert 600,25 mit der Zahl, aus der die Wurzel gezogen werden soll, also mit 49. 600,25 ist deutlich größer als 49. Denach ist 24,5 als Wurzel zu groß. Die gesuchte Wurzel muss kleiner sein, liegt also zwischen 0 und 24,5.
- Die rechte Grenze wird nun zu 24,5 geändert.
- Die nächste Berechnung geht bei Nummer 2 weiter.
Die Schritte 2-6 müssen nun oft genug durchgeführt werden. Das ist aber für den Calliope mini kein Problem: man nutzt einfach eine Zählschleife.
Im konkreten Fall wird die Berechnung 100 Mal durchgeführt. Am Ende wird die rechte Grenze ausgegeben: es erscheint die Zahl 7. Prima.
Setzt man die Schrittanzahl auf z.B. 10, wird die Berechnung zu zeitig abgebrochen und die ausgegebene Wurzel ist etwas größer als 7.
Die Idee für den ersten Teil stammt aus der Zeitschrift c’t, Ausgabe 12/2022, Seite 156 ff.
kontrollierter Abbruch
Wie oft muss nun aber die Schleife mindestens durchlaufen werden, damit die exakte Wurzel berechnet wird. An Stelle des geschätzten 100-fachen Durchlaufes wird die Schleife durch eine kontrollierte Abbruchbedingung nur sooft durchlaufen, wie es wirklich notwendig ist. Nach jeder Schleife wird ein Zähler um eins erhöht und zum Schluss nach der Ausgabe der Wurzel angezeigt. Im konkreten Fall sind das 55 Durchläufe! Wer das Programm im Debugmodus bei der Arbeit zuschaut, stellt fest, dass die Wurzel eigentlich schon viel früher feststeht. Der Calliope mini arbeitet aber mit Zahlen, die über 13 Kommastellen haben und erst nach 55 Schritten kommt er dazu, dass auch die letzte Kommastelle eine 0 wird.
Falls man als Zahl, aus der die Wurzel gezogen werden soll, eine 37 eingibt, erhält man kein Ergebnis. Das Programm hängt.

Wurzel aus jeder Zahl
Wieviel Schleifendurchläufe braucht man nun aber, um die Wurzel aus einer Zahl zu bestimmen, die keine Quadratzahl ist. Eigentlich solange, bis der rechte Wert mit dem linken Wert übereinstimmen. So einfach geht das aber nicht.
Wie groß ist z.B. die Wurzel aus 37? Aus 36 ist sie eindeutig 6. Die Wurzel aus 37 ist eine irrationale Zahl. Das heiß vereinfacht: sie hat eine unendliche große Menge an Kommastellen. Deshalb kann man nicht solange rechnen, bist rechts und links gleich sind. Das sind sie nie! Es gibt keine Zahl, die quadriert genau 37 ergibt.
Deshalb muss man bereits vor der Berechnung wissen, auf wieviel Nachkommastellen die Wurzel berechnet werden soll. Es muss einen kontrollierten Abbruch der Schleife geben.
Die Wurzel aus 37 soll mit zwei Kommastellen ausgegeben werden. Dazu wird die Differenz der beiden Werte rechts und links mit einer Grenze verglichen. Die Grenze wird aus der Anzahl der Kommastellen berechnet und ist hier 0,001. Die beiden Werte sind also nicht gleich, sondern unterscheiden sich um 0,001.
Nach der Berechnung wird die Wurzel aus dem Wert rechts mit den gewünschten Kommastellen angezeigt.

Wurzel aus Quadratzahlen
Das Halbierungsverfahren kann für verschiedene mathematischen Probleme verwendet werden. Hier wird es für das Ziehen einer Wurzel aus einer beliebigen Zahl benutzt.
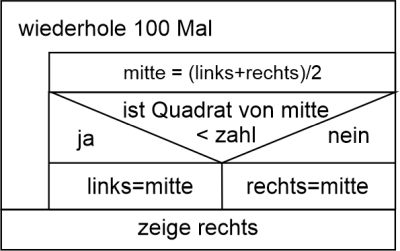
Es soll am Ziehen der Wurzel aus 49 beschrieben werden. Wir wissen, dass das Ergebnis 7 ist. Nur der Calliope mini weiß das nicht und muss deshalb die Wurzel berechnen.
- Es werden zwei Zahlen bestimmt, zwischen denen das Ergebnis auf jeden Fall liegt. Das sind in diesem Fall die beiden Zahlen 0 und 49. Die 0 nennen wir linke Grenze (links) und die 49 rechte Grenze (rechts).
- Es wird die Mitte zwischen diesen beiden Zahl berechnet: mitte=(links+rechts)/2. In diesem Fall ist das 24,5
- Von dem Wert mitte wird das Quadrat berechnet. 24,5² = 600,25
- Jetzt vergleicht man den Wert 600,25 mit der Zahl, aus der die Wurzel gezogen werden soll, also mit 49. 600,25 ist deutlich größer als 49. Denach ist 24,5 als Wurzel zu groß. Die gesuchte Wurzel muss kleiner sein, liegt also zwischen 0 und 24,5.
- Die rechte Grenze wird nun zu 24,5 geändert.
- Die nächste Berechnung geht bei Nummer 2 weiter.
Die Schritte 2-6 müssen nun oft genug durchgeführt werden. Das ist aber für den Calliope mini kein Problem: man nutzt einfach eine Zählschleife.
Im konkreten Fall wird die Berechnung 100 Mal durchgeführt. Am Ende wird die rechte Grenze ausgegeben: es erscheint die Zahl 7. Prima.
Setzt man die Schrittanzahl auf z.B. 10, wird die Berechnung zu zeitig abgebrochen und die ausgegebene Wurzel ist etwas größer als 7.

Die Idee für den ersten Teil stammt aus der Zeitschrift c’t, Ausgabe 12/2022, Seite 156 ff.
kontrollierter Abbruch
Wie oft muss nun aber die Schleife mindestens durchlaufen werden, damit die exakte Wurzel berechnet wird. An Stelle des geschätzten 100-fachen Durchlaufes wird die Schleife durch eine kontrollierte Abbruchbedingung nur sooft durchlaufen, wie es wirklich notwendig ist. Nach jeder Schleife wird ein Zähler um eins erhöht und zum Schluss nach der Ausgabe der Wurzel angezeigt. Im konkreten Fall sind das 25 Durchläufe!
Falls man als Zahl, aus der die Wurzel gezogen werden soll, eine 37 eingibt, erhält man kein Ergebnis. Das Programm hängt.

Wurzel aus jeder Zahl
Wieviel Schleifendurchläufe braucht man nun aber, um die Wurzel aus einer Zahl zu bestimmen, die keine Quadratzahl ist. Eigentlich solange, bis der rechte Wert mit dem linken Wert übereinstimmen. So einfach geht das aber nicht.
Wie groß ist z.B. die Wurzel aus 37? Aus 36 ist sie eindeutig 6. Die Wurzel aus 37 ist eine irrationale Zahl. Das heiß vereinfacht: sie hat eine unendliche große Menge an Kommastellen. Deshalb kann man nicht solange rechnen, bist rechts und links gleich sind. Das sind sie nie! Es gibt keine Zahl, die quadriert genau 37 ergibt.
Deshalb muss man bereits vor der Berechnung wissen, auf wieviel Nachkommastellen die Wurzel berechnet werden soll. Es muss einen kontrollierten Abbruch der Schleife geben.
Die Wurzel aus 37 soll mit zwei Kommastellen ausgegeben werden. Dazu wird die Differenz der beiden Werte rechts und links mit einer Grenze verglichen. Die Grenze wird aus der Anzahl der Kommastellen berechnet und ist hier 0,001. Die beiden Werte sind also nicht gleich, sondern unterscheiden sich um 0,001.
Nach der Berechnung wird die Wurzel aus dem Wert rechts mit den gewünschten Kommastellen angezeigt.
Als Ergebnis für die Wurzel aus 37 wird 6.08 ausgegeben.
Hinweis: Falls man die Ausgabe nicht rundet, erhält man mehr Kommastellen. Davon sind aber nur die ersten beiden richtig.

Mit dem Halbierungsverfahren lassen sich auch andere Funktionen realisieren. Z.B. ist jede andere Wurzel aus einer Zahl zu ziehen (3.Wurzel...n. Wurzel).

 Campus
Campus  Make Code
Make Code  Open Roberta Lab
Open Roberta Lab  Python
Python 