Quersumme
Quersumme aus einer vierstelligen Zahl...
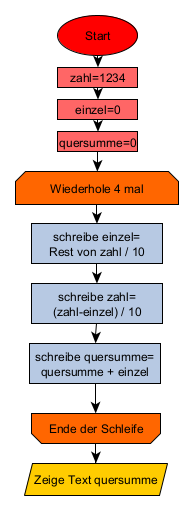
Zum Bilden der Quersumme werden in jeweils drei Schritten die einzelnen Ziffern von hinten an abgetrennt und summiert.
- Die Zahl wird ganzzahlig durch 10 geteilt. Der Rest der Division wird in der Variable einzel abgelegt.
1234/10 = 123 und der Rest ist 4. - Von der Zahl wird die 4 abgezogen (1234-4=1230) und das Ergebnis durch 10 geteilt (1230/10=123)
- Die 4 wird zur Variablen quersumme addiert.
Danach wird die ganze Prozedur mit der Zahl 123 wiederholt. In der Variablen zahl der dann Wert 12. Nach den 4 Wiederholungen erhält man als Quersumme das Ergebnis 10.
...und mit beliebiger Stellenzahl
Will man die Quersumme einer fünfstelligen Zahl bilden (z.B. 11111), muss die Anzahl der Wiederholungen auf 5 gesetzt werden. Das ist umständlich. Abhilfe schafft ein Befehl, der aus der zahl selber die Stellenzahl bestimmt.
Die Funktion ![]() (Logarithmus 10) findet eine Zahl x, so dass gilt: 10x=zahl. Für die Zahl 1234 liefert die Funktion 3,09. Rundet man das auf, erhält man 4 und hat die Anzahl der Stellen.
(Logarithmus 10) findet eine Zahl x, so dass gilt: 10x=zahl. Für die Zahl 1234 liefert die Funktion 3,09. Rundet man das auf, erhält man 4 und hat die Anzahl der Stellen.

Im Prinzip geht es,...
aber beim Testen fällt auf, dass für die Zahl 1000 als Quersumme eine 0 geliefert wird. Das ist eindeutig falsch!
Was ist die Ursache?
Der Logarithmus von 1000 liefert als Ergebnis eine 3. Die ist aber aufgerundet immer noch eine 3. Deshalb wird die Schleife nur drei Mal durchlaufen, also 0+0+0.
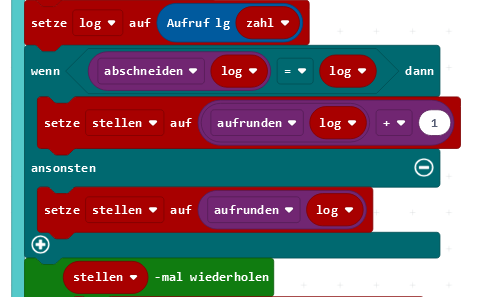
Vor der Berechnung der Quersumme muss man also prüfen, ob der Logarithmus der Zahl eine ganze Zahl ist. Falls das der Fall ist, wird die Stellenzahl um 1 erhöht.
![]()
Quersumme aus einer vierstelligen Zahl...
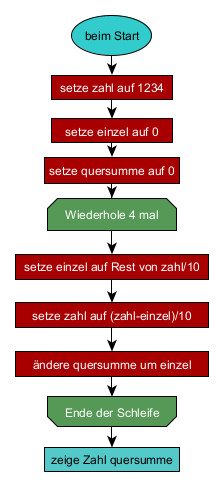
Zum Bilden der Quersumme werden in jeweils drei Schritten die einzelnen Ziffern von hinten an abgetrennt und summiert.
- Die Zahl wird ganzzahlig durch 10 geteilt. Der Rest der Division wird in der Variable einzel abgelegt.
1234/10 = 123 und der Rest ist 4. - Von der Zahl wird die 4 abgezogen (1234-4=1230) und das Ergebnis durch 10 geteilt (1230/10=123)
- Die 4 wird zur Variablen quersumme addiert.
Danach wird die ganze Prozedur mit der Zahl 123 wiederholt. In der Variablen zahl der dann Wert 12. Nach den 4 Wiederholungen erhält man als Quersumme das Ergebnis 10.
...und mit beliebiger Stellenzahl
Will man die Quersumme einer fünfstelligen Zahl bilden (z.B. 11111), muss die Anzahl der Wiederholungen auf 5 gesetzt werden. Das ist umständlich. Abhilfe schafft ein Befehl, der aus der zahl selber die Stellenzahl bestimmt.
Der Logarithmus zur Basis 10 findet eine Zahl x, so dass gilt: 10x=zahl (Klingt kompliziert, weiterlesen!). Für die Zahl 1234 liefert die Funktion lg(1234)=3,09, weil 103,06=1234 ist.. Rundet man das auf, erhält man 4 und hat die Anzahl der Stellen.
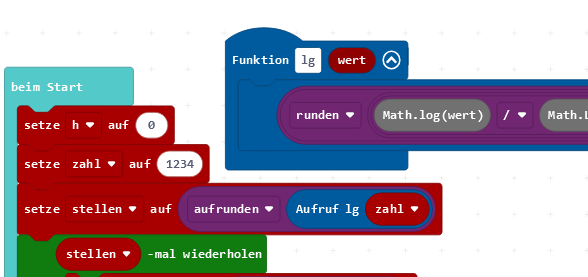
Im Prinzip geht es,...
aber beim Testen fällt auf, dass für die Zahl 1000 als Quersumme eine 0 geliefert wird. Das ist eindeutig falsch!
Was ist die Ursache?
Der Logarithmus von 1000 liefert als Ergebnis eine 3. Die ist aber aufgerundet immer noch eine 3. Deshalb wird die Schleife nur drei Mal durchlaufen, also 0+0+0.
Vor der Berechnung der Quersumme muss man also prüfen, ob der Logarithmus der Zahl eine ganze Zahl ist. Falls das der Fall ist, wird die Stellenzahl um 1 erhöht.
Einstellige (oder iterierte) Quersumme
Von der Quersumme wird wieder die Quersumme gebildet. Das macht man solange, bis man eine einstellige Zahl erhält. Auch hier ist klar, dass man am Anfang nicht weiß, wie oft man die Quersumme bilden muss. Von der Zahl 1233 ist die Quersumme sofort einstellig 9, von der Zahl 1234 ist die Quersumme 10.
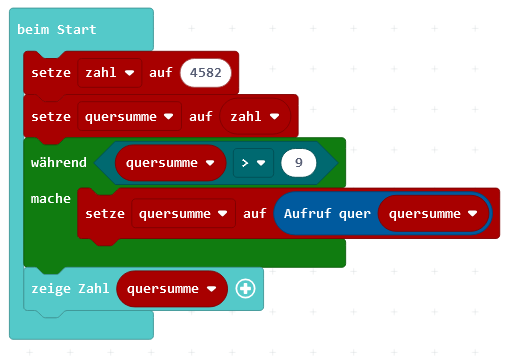
Deshalb wird die Quersummenbildung in eine Funktion ausgelagert und die Funktion so oft aufgerufen, bis das Ziel erreicht ist. Der Aufruf erfolgt in einer bedingten Schleife. Solange eine Bedingung erfüllt ist, wird die Schleife durchlaufen. Die Funktion zur Berechnung der Quersumme wird also solange immer wieder aufgerufen, solange die erhaltene Quersumme größer als 9 ist.
Wenn alles funktioniert, erhält man bei der Beispielzahl die einstellige Quersumme 1. Das Programm kann genutzt werden, um die Richtigkeit einer eingegebenen Zahl zu prüfen (Prüfzahl).
Es geht auch viel einfacher
Die Zahl, von der die Quersumme bestimmt werden soll, wird zuerst in einen String (Text) umgewandelt. Jetzt kann man damit zwar nicht mehr rechnen, aber über die Textfunktionen schön zerlegen.
Es lässt sich z.B. über die entsprechende Funktion die Länge der Zeichenkette bestimmen. Die ist in diesem Fall 4.
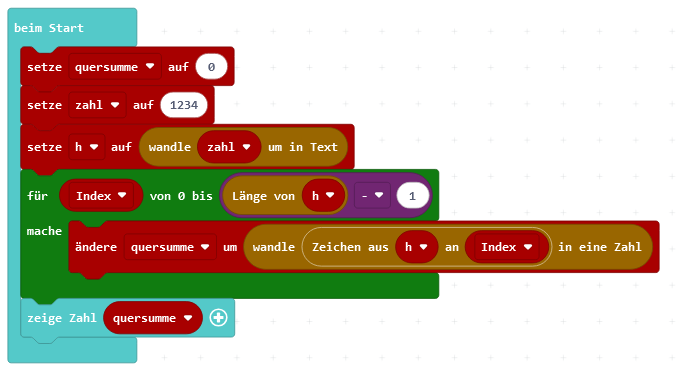
Danach kann man auf jedes einzelne Zeichen über seine Positionsnummer zugegriffen werden. Die 1 hat die Nummer 0, die 2 die Nummer 1 usw. Da man mit dem Zählen bei 0 beginnt, hat die letzte Ziffer die Nummer 3. Deshalb darf man nur bis Länge -1 zählen.
Jetzt hat man das einzelne Zeichen aus der ganzen Zahl herausgelöst, wandelt es wieder in eine Ziffer um (mit der kann man rechnen!) und addiert es zur Variablen quersumme dazu.
Fertig.
Quersumme aus einer Zahl
Das Programm zum Berechnen der Quersumme ist mit Kommentar ganze 7 Zeilen lang! Die Zahl, aus der die Quersumme bestimmt werden soll, wird in einen String (Text) umgewandelt.
Die for-Schleife läuft automatisch den String entlang und weist der Variablen einzel jede einzelne Stelle aus der Variablen zahl zu. Das ist total einfach!
Damit der Inhalt der Variable einzel zur Quersumme addiert werden kann, muss er vorher wieder in eine Zahl umgewandelt werden. Das erfolgt über die Funktion int().

Einstellige (oder iterierte) Quersumme
Von der Quersumme wird wieder die Quersumme gebildet. Das macht man solange, bis man eine einstellige Zahl erhält. Auch hier ist klar, dass man am Anfang nicht weiß, wie oft man die Quersumme bilden muss. Von der Zahl 1233 ist die Quersumme sofort einstellig 9, von der Zahl 1234 ist die Quersumme 10.
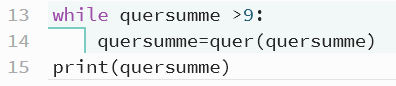
Deshalb wird die Quersummenbildung in eine Funktion quer(zahl) ausgelagert und die Funktion so oft aufgerufen, bis das Ziel erreicht ist. Der Aufruf erfolgt in einer bedingten Schleife. Solange eine Bedingung erfüllt ist, wird die Schleife durchlaufen. Die Funktion zur Berechnung der Quersumme wird also solange immer wieder aufgerufen, solange die erhaltene Quersumme größer als 9 ist.
Wenn alles funktioniert, erhält man bei der Beispielzahl die einstellige Quersumme 1. Das Programm kann genutzt werden, um die Richtigkeit einer eingegebenen Zahl zu prüfen (Prüfzahl).

 Campus
Campus  Make Code
Make Code  Open Roberta Lab
Open Roberta Lab  Python
Python 