Bubblesort
1. Anzeige der Zahlen
In einem Array werden fünf Zahlen abgelegt, die zwischen 1 und 5 liegen. Die Zahlenwerte werden auf dem Bildschirm als Säulen angezeigt.
Hinweis: Die j-Schleife zählt von 0 bis eine Zahl vor dem Eintrag im Array-Element. Im ersten Fall wird die Schleife also nur ein Mal durchlaufen und die LED bei 4-0=4 eingeschaltet.

2. Taste A
Im nächsten Schritt werden die eben geschriebenen Anzeigebefehle in einer Funktion abgelegt. Das macht das Programm dann übersichtlicher.
Dann wird die Taste A dazu verwendet, bei jedem Druck die Anzeige zu aktualisieren und die Farbe der LED zu wechseln. Die eigentliche Sortierung erfolgt im nächsten Schritt vor der Aktualisierung der Anzeige.

3. Tauschen
Es werden nun im Array die ersten beiden Werte miteinander verglichen. Falls der erste Wert größer als der zweite Wert ist, werden beide Einträge getauscht. Damit rutscht eine größere Zahl eine Position nach rechts, also zum Ende des Arrays hin.
Danach wird der Zähler um eins erhöht und die nächsten beiden Einträge im Array miteinander verglichen. Die größere Zahl von diesen beiden wird wieder nach rechts geschoben. Damit wandert eine große Zahl Schritt für Schritt nach rechts.
Wichtig: In dem Programmblock, der beim Loslassen der Taste A ausgeführt wird, muss überprüft werden, ob die Variable zaehler nicht größer als 4 wird. Falls das der Fall ist, muss sie auf 0 zurückgesetzt werden, sie darf also den Wert 5 nie erreichen.

Bei jedem Druck auf die Taste A werden zwei benachbarte Zahlen verglichen und bei Bedarf getauscht. Zum Schluss stehen die 5 Zahlen schön geordnet da.
4. Mit Schleifen arbeiten
Wenn man den Programmteil zum Tauschen von einer Schleife mehrmals aufrufen lässt, kann man bei jedem Drücken der Taste A das Array einmal durchwandern und die größte Zahl nach rechts wandern lassen.
Ruft man den Tauschprozess mit einer weiteren Schleife vier Mal auf, wird das Array in einem Rutsch geordnet.
Das Video zeigt den schlimmsten Fall: zu Beginn sind alle Zahlen verkehrt herum geordnet. Ein Knopfdruck und alles hat seine Ordnung.
Da das Prinzip jetzt bekannt sein dürfte, kann man größere Arrays ordnen lassen. Als Anzeige ist der Calliope-Monitor nun aber nicht mehr geeignet. Besser ist der seriell Monitor aus der Arduino-IDE.
Da die komplette Anzeige in einer Fuktion steht, kann man entweder die Funktion ändern oder eine neue Anzeigefunktion schreiben.
Nun kann man ordentlich in die Vollen gehen. Im Beispiel besteht das Array aus 30 Zufallszahlen zwischen 1 und 150.
1. Anzeige der Zahlen
In einem Array werden fünf Zahlen abgelegt, die zwischen 1 und 5 liegen. Die Zahlenwerte werden auf dem Bildschirm als Säulen angezeigt.
Hinweis: Die j-Schleife zählt von 0 bis zu der Zahl , die in dem Array-Element steht. Im ersten Fall wird die Schleife also zwei Mal durchlaufen. Da aber nur eine LED eingeschaltet werden soll, muss vom Wert noch 1 abgezogen werden.

2. Taste A
Im nächsten Schritt werden die eben geschriebenen Anzeigebefehle in einer Funktion abgelegt. Das macht das Programm dann übersichtlicher.
Dann wird die Taste A dazu verwendet, bei jedem Druck die Anzeige zu aktualisieren. Die eigentliche Sortierung erfolgt im nächsten Schritt vor der Aktualisierung der Anzeige.
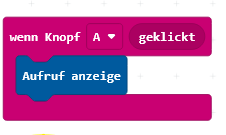
3. Tauschen
Es werden nun im Array die ersten beiden Werte miteinander verglichen. Falls der erste Wert größer als der zweite Wert ist, werden beide Einträge getauscht. Damit rutscht eine größere Zahl eine Position nach rechts, also zum Ende des Arrays hin.
Damit z.B. die erste Zahl ganz nach hinten rutscht, muss sie 4 Mal mit ihrem rechten Nachbarn getauscht werden. Man benötigt einen Zähler von 0 bis 3! Bevor der eigentliche Tausch programmiert wird, testet man diesen Zähler.
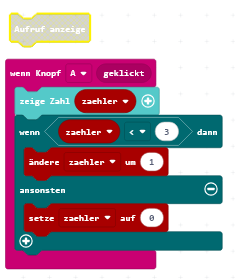
Beim Tausch wird die Zahl von der Position zaehler in die Variable zahl_1 geschrieben und die darauf folgende Zahl (zaehler+1) in die Variable zahl_2. Ist die erste Zahl größer als die zweite Zahl, werden beide getauscht und die Inhalte des Array sofort angezeigt. Danach wird, wie beschrieben, die Variable zaehler verändert.
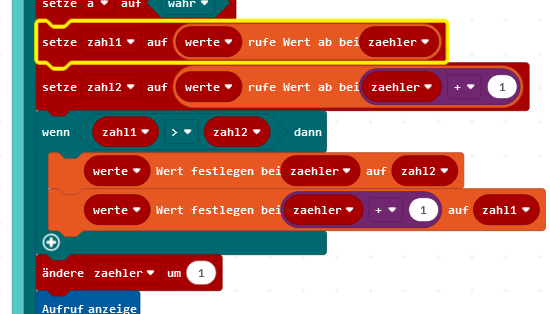
Bei jedem Druck auf die Taste A werden zwei benachbarte Zahlen verglichen und bei Bedarf getauscht. Zum Schluss stehen die 5 Zahlen schön geordnet da.
4. Mit Schleifen arbeiten
Wenn man den Programmteil zum Tauschen von einer Schleife mehrmals aufrufen lässt, kann man bei jedem Drücken der Taste A das Array einmal durchwandern und die größte Zahl nach rechts wandern lassen. Das sieht dann nicht mehr so schön wie vorher aus, geht aber schneller.
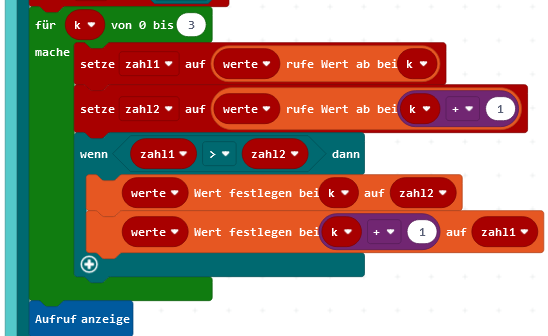
Das Video zeigt den schlimmsten Fall: zu Beginn sind alle Zahlen verkehrt herum geordnet. Bei jedem Kopfdruck wandert die größte nach rechts an ihren richtigen Platz.
Ruft man den Tauschprozess mit einer weiteren Schleife vier Mal auf (4-mal wiederholen) , wird das Array in einem Rutsch geordnet.
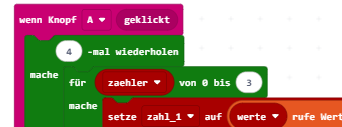
Große Listen ordnen
Da das Prinzip jetzt bekannt sein dürfte, kann man größere Arrays ordnen lassen. Um möglichst flexibel zu sein, werden in den beiden eben eingefügten Zählschleifen die Zahlen durch berechnete Werte aus der Länge des Array berechnet.
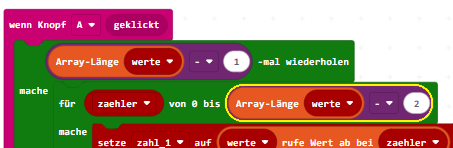
Jetzt braucht man noch eine ordentliche Anzeige, das Display des Calliope mini ist nicht mehr geeignet.

Nun kann man ordentlich in die Vollen gehen. Im Beispiel besteht das Array aus 30 Zufallszahlen zwischen 1 und 150.

5.Bubblesort grafisch anzeigen
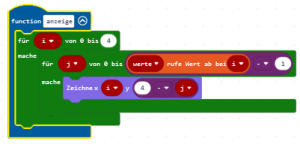
Über die Erweiterung oledpaint lassen sich senkrechte Linien auf dem Display darstellen. Wenn man die Anzeigefunktion entsprechend umgestaltet, lassen sich die Zahlen im Array in Linien verschiedener Länge anzeigen.
Im konkreten Beispiel bestand das Array aus 128 Einträgen. In jedem Eintrag stand eine Zufallszahl zwischen 0 und 63. Zu Beginn ist das Array völlig ungeordnet und am Ende stehen die großen Zahlen hinten und die Kleinen ganz vorn.
1. Anzeige der Zahlen
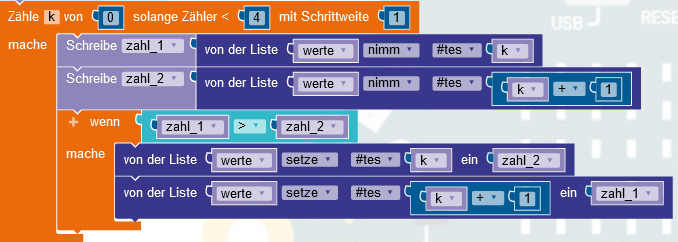
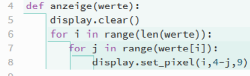
In einer Liste werte werden fünf Zahlen abgelegt, die zwischen 1 und 5 liegen. Die Zahlenwerte werden auf dem Bildschirm als Säulen angezeigt.
Die erste Schleife läuft von 0 bis 4, da genau 5 Zahlen in der Liste stehen.
len(werte) liefert eine 5, da die Liste werte 5 Elemente hat. Die range()-Funktion liefert aber eine Zahlenfolge von 0 bis 4. Der Wert, der der range()-Funktion übergeben wird, also die 5, ist in der Folgen nicht mehr enthalten. Das klingt zwar unlogisch, ist aber für das Arbeiten mit Listen eine clevere Sache. Eine Liste mit 5 Elementen enthält ja auch die Elemente mit den Nummern 0 bis 4. Damit liefert die range()-Funktion genau die Nummern der Elemente.
Die Anzahl der Durchläufe der zweiten Schleife hängt vom Inhalt des Elementes ab, das durch die erste Schleife ausgewählt wurde. Beim ersten Mal geht es also um das Element mit der Nummer 0. Der Inhalt ist eine 1. Die range()-Funktion liefert nur eine 0 zurück und es wird in der ersten Spalte (x=0) die unterste LED mit der Helligkeit 9 eineschaltet.
Wird die Schleife beim zweiten Durchlauf der ersten Schleife erreicht, steht in der Liste der Wert 5. Damit wird die zweite Schleife von j=0 bis j=4 durchlaufen, also 5 Mal. Es werden die 5 LEDs der zweiten Spalte komplett eingeschaltet.

2. Taste A
Im nächsten Schritt werden die eben geschriebenen Anzeigebefehle in einer Funktion abgelegt. Das macht das Programm dann übersichtlicher. Der Funktion wird die Liste, die die Werte enthält, übergeben. Damit es nicht zu Verwechslungen kommt, nennt man die Liste der Zahlen jetzt liste.
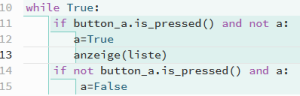
Dann wird die Taste A dazu verwendet, bei jedem Druck die Anzeige zu aktualisieren. Die Variable a sichert, dass beim Druck auf A die folgenden Befehle nur einmal ausgeführt werden. Dazu ist a zu Beginn des Programms auf False zu setzen.
Die eigentliche Sortierung erfolgt im nächsten Schritt vor der Aktualisierung der Anzeige.
3. Tauschen
Beim ersten Drücken der Taste A werden im Array die ersten beiden Werte miteinander verglichen. Dazu ist eine Variable zaehler zu Beginn des Programms auf 0 zu setzen.
Falls der erste Wert größer als der zweite Wert ist, werden beide Einträge getauscht. Damit rutscht eine größere Zahl eine Position nach rechts, also zum Ende des Arrays hin.
Danach wird der Zähler in dem Programmteil, der beim Loslassen der Taste A ausgeführt wird, um eins erhöht und die nächsten beiden Einträge im Array miteinander verglichen. Die größere Zahl von diesen beiden wird wieder nach rechts geschoben. Damit wandert eine große Zahl Schritt für Schritt nach rechts.
Wichtig:es muss immer geprüft werden, ob die Variable zaehler nicht größer als 4 wird. Falls das der Fall ist, muss sie auf 0 zurückgesetzt werden, sie darf also den Wert 5 nie erreichen. Falls doch, gibt es eine Fehlermeldung, da auf einen Wert zugegriffen werden soll, der nicht existiert.

Bei jedem Druck auf die Taste A werden zwei benachbarte Zahlen verglichen und bei Bedarf getauscht. Zum Schluss stehen die 5 Zahlen schön geordnet da.
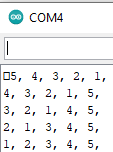
Im Beispiel wurde die Zahlenfolge 5,2,3,4,1 verwendet. Die Taste A muss 13 Mal gedrückt werden, bis die Reihe geordnet ist.
4. Mit Schleifen arbeiten
Wenn man den Programmteil zum Tauschen von einer Schleife mehrmals aufrufen lässt, kann man bei jedem Drücken der Taste A das Array einmal durchwandern und die größte Zahl nach rechts wandern lassen. Zum Schluss steht die größte Zahl ganz rechts.
Damit man den Prozess verfolgen kann, wird die Anzeige in jedem Schleifendurchlauf aufgerufen und eine halbe Sekunde gewartet.

Ruft man den Vorgang, der die größte Zahl nach rechts wandern lässt, sooft auf, wie Elemente in der Liste sind, hat man zum Schluss eine geordnete Liste. Die innere Schleife muss bei jedem Durchlauf der äußeren Schleife nicht mehr für alle Elemente durchlaufen werden, da ja die größte Zahl schon ganz rechts steht nun nicht mehr beachtet werden. Deswegen wird die innere Schleife bei jedem Durchlauf der äußeren Schleife um eins weniger durchlaufen.

Im Video wird beim Start die Liste mit dem schlimmsten aller Fälle gefüllt: 5,4,3,2,1. (Worst Case (schlechtester Fall ~ die Werte sind „maximal ungünstig “). Ein Druck auf die A-Taste bringt alles schnell in die gewünschte Ordnung.
große Listen sortieren
Eine Liste mit 5 Elementen lässt sich leicht per Hand sortieren. Bei vielen Elementen ist das schon schwieriger.
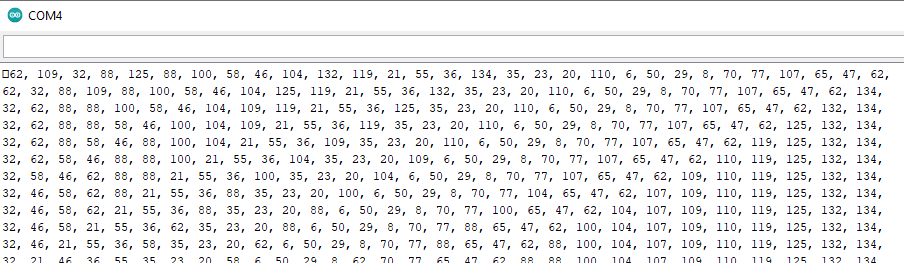
Zu Beginn des Programms wird in einer Schleife eine Liste zufällig mit Zahlen zwischen 1 und 100 gefüllt. Die Anzeige kann jetzt natürlich nicht mehr so schön in einem Balkendiagramm erfolgen. Die Zahlen werden durch den print-Befehl als serielle Daten angezeigt.
Am Sortierteil des Programms muss nichts geändert werden. Da man sich konsequent in den Schleifen auf die Länge der Liste bezieht, laufen die eben nicht 5 Mal, sondern 100 Mal.
Die Ausgabe muss jetzt auch wieder über den print-Befehl realisiert werden.

5. Zeitkomplexität
Unter der Zeitkomplexität versteht man die Anzahl der notwendigen Tauschoperationen, bis eine Liste vollständig geordnet ist. Da der Nutzer grundsätzlich ungeduldig ist, muss ein Sortierverfahren möglichst schnell durchgeführt werden.
Dabei geht es nicht um die eigentliche Rechenzeit, sondern den Zusammenhang zwischen dem Zeitbedarf und der Anzahl der Datenmenge.
Konkret: Wie ändert sich die Zeit, wenn die Datenmenge verdoppelt wird, Verdoppelt sie sich auch?
Dazu wird die Zeit bestimmt, die für das Sortieren einer Liste benötigt wird. In der Variablen start wird vor dem Sortieren die aktuelle Zeit bestimmt und nach dem Sortieren wird diese Zeit von der aktuellen Zeit abgezogen. Dadurch erhält man die eigentliche Laufzeit des Sortiervorganges.
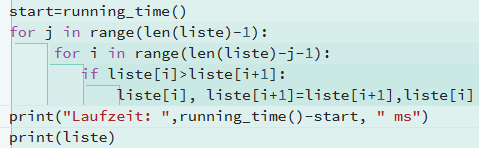
Für die 100 Elemente benötigt der Calliope mini etwa 400 ms. Was passiert, wenn man die Anzahl der Elenemte verdoppelt?
Bei doppelt sovielen Zahlen arbeitet das Programm etwa 1600 ms. Eine Verdopplung der Elementezahl bedeutet eine Vervierfachung der Zeit.
Wenn zwischen Zeit und Anzahl der Zahlen ein quadratischer Zusammenhang existiert, sollten z.B. 500 Zahlen in etwa 10 000 ms, also 10 s, geordnet sein. Ausprobieren!
Jetzt kann man noch untersuchen, ob die Reihenfolge der unsortierten Zahlen eine Auswirkung auf die Zeit hat. Man unterscheidet drei Fälle
- Günstigster Fall (Best-Case): Die Zahlen sind schon geordnet
- Mittlerer Fall (Average Case): Die Zahlen sind zufällig verteilt (das ist üblich)
- Ungünstigster Fall (Worst-Case): Die Zahlen stehen genau in entgegengesetzter Sortierreihenfolge in der Liste.
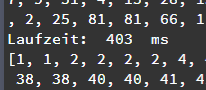
Für die 200 Zahlen hat man vorhin schon die Zeit für den mittleren Fall zu etwa 1600 ms bestimmt.
Ändert man das Erstellen der Liste, ist sie bereits zu Beginn geodnet und die Laufzeit des Programms beträgt nur noch etwa 1000 ms. Die schlimmste Ausgangssituation erhält man mit liste.append(anzahl-i). Dann dauert der Sortiervorgang etwa 2300 ms.


 Campus
Campus  Make Code
Make Code  Open Roberta Lab
Open Roberta Lab  Python
Python 