Wasserwaage 2
Hinweis: Im OpenRobertaLab und in Make Code sind die x- und y-Achsen anders belegt!
Es werden die bei Flugzeugen üblichen Begriffe verwendet: Rollen und Nicken. Der Gierwinkel wird leider von keiner Entwicklungsumgebung abgefragt (Mai 2022).
Wenn der Bug (Vorderseite) des Calliope mini am USB-Anschluss liegt, dann ist Rollen eine Bewegung um die y-Achse und Nicken eine Bewegung um die x-Achse.
Beachte: Die x-Achse verläuft beim Calliope mini vom Pin 0 zum Pin 3, die y-Achse von unten nach oben (USB-Anschluss).
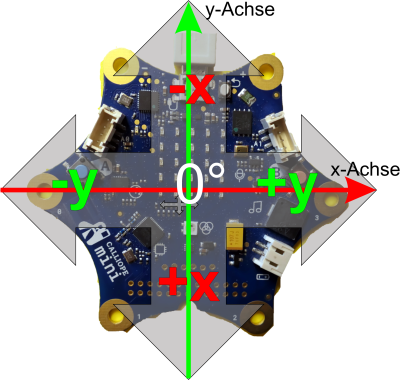
Wie bei der Wasserwaage 1 wird der x- Wert (Nicken) in einer Variablen abgelegt. Waagerecht bedeutet genau 0° und die Abweichugen nach vorn und hinten liefern Absolutwerte größer als 0°. Das Vorzeichen des Rollwinkels sagt etwas über die Richtung aus: Plus nach hinten und Minus nach vorn. Das kann man sich sehr schön im seriellen Plotter auschauen.
Da bei der Wasserwaage beide Achsen berücksichtig werden sollen, muss noch der y-Wert (Rollen) abgefragt werden und in die Entscheidung mit einfließen. Genau waagerecht liefert 0°. Die Neigung aus der Waggerechten liefert Absolutwerte größer als 0°. Das Vorzeichen der Neigung sagt etwas über die Richtung aus: Plus nach rechts und Minus nach links.
Das Bild zeigt die Anzeige im seriellen Plotter f?r den x-Wert, wenn der Calliope mini um die x-Achse bewegt wird. Im letzten Teil liegt er waagerecht.

Es wird wieder eine Empfindlichkeit festgelegt. Ist sie z.B. 10° groß, leuchtet die mittlere LED (x=2, y=2) bei
- Nicken zwischen -10° und 10°
- Rollen zwischen -10° und 10°
Die jeweils daneben liegende LED leuchtet bei einer Abweichung zwischen 10° und 20° auf, die noch weiter außen liegende dann bei einer Abweichung zwischen 20° und 30°.
Aus den Variablen nicken und rollen lassen sich die Koordinaten der LED berechnen, die aufleuchten sollen.
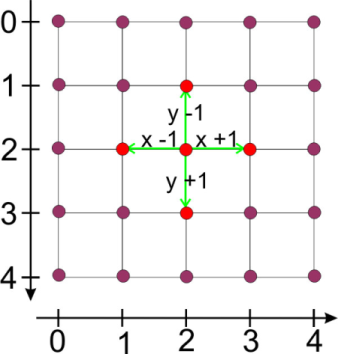

Die Abblidung zeigt die Berechnung der Zeilen- und Spaltenwerte bei einer Drehung. Um das zu Verstehen, sollte man die Rechung für einige Drehwinkel per Hand durchführen.
| Drehwinkel | /empf | runden | berechneter x-Wert |
|---|---|---|---|
| 1? | 0,1 | abrunden: 0 | 2 |
| 9° | 0,9 | abrunden: 0 | 2 |
| 11° | 1,1 | abrunden: 1 | 1 |
| -1° | -0,1 | aufrunden: 0 | 2 |
| -9° | -0,9 | aufrunden: 0 | 2 |
| -11° | -1,1 | aufrunden: -1 | 1 |
Beachte: Wenn man -1,1 aufrundet, erhält man -1!
Es werden die bei Flugzeugen üblichen Begriffe verwendet: Rollen und Nicken. Der Gierwinkel wird leider von keiner Entwicklungsumgebung abgefragt (Mai 2022).
Wenn der Bug (Vorderseite) des Calliope mini am USB-Anschluss liegt, dann ist Rollen eine Bewegung um die x-Achse und Nicken eine Bewegung um die y-Achse.
Beachte: Die y-Achse verläuft beim Calliope mini vom Pin 0 zum Pin 3, die x-Achse von unten nach oben (USB-Anschluss).
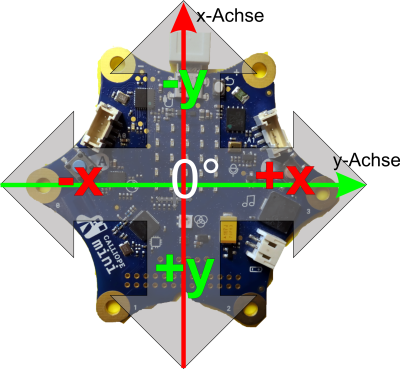
Wie bei der Wasserwaage 1 wird der y- Wert (Nicken) in einer Variablen abgelegt. Waagerecht bedeutet genau 0° und die Abweichugen nach vorn und hinten liefern Absolutwerte größer als 0°. Das Vorzeichen des Rollwinkels sagt etwas über die Richtung aus: Plus nach hinten und Minus nach vorn. Das kann man sich sehr schön im seriellen Plotter auschauen.
Da bei der Wasserwaage beide Achsen berücksichtig werden sollen, muss noch der x-Wert (Rollen) abgefragt werden und in die Entscheidung mit einfließen. Genau waagerecht liefert 0°. Die Neigung aus der Waggerechten liefert Absolutwerte größer als 0°. Das Vorzeichen der Neigung sagt etwas über die Richtung aus: Plus nach rechts und Minus nach links.
Das Bild zeigt die Anzeige im seriellen Plotter f?r den y-Wert, wenn der Calliope mini um die y-Achse bewegt wird. Im letzten Teil liegt er waagerecht.

Es wird wieder eine Empfindlichkeit festgelegt. Ist sie z.B. 10° groß, leuchtet die mittlere LED (x=2, y=2) bei
- Nicken zwischen -10° und 10°
- Rollen zwischen -10° und 10°
Die jeweils daneben liegende LED leuchtet bei einer Abweichung zwischen 10° und 20° auf, die noch weiter außen liegende dann bei einer Abweichung zwischen 20° und 30°.
Aus den Variablen nicken und rollen lassen sich die Koordinaten der LED berechnen, die aufleuchten sollen.


Die Abblidung zeigt die Berechnung der Zeilen- und Spaltenwerte bei einer Drehung. Um das zu Verstehen, sollte man die Rechung für einige Drehwinkel per Hand durchführen.
| Drehwinkel | /empf | runden | berechneter x-Wert |
|---|---|---|---|
| 1? | 0,1 | abrunden: 0 | 2 |
| 9° | 0,9 | abrunden: 0 | 2 |
| 11° | 1,1 | abrunden: 1 | 1 |
| -1° | -0,1 | aufrunden: 0 | 2 |
| -9° | -0,9 | aufrunden: 0 | 2 |
| -11° | -1,1 | aufrunden: -1 | 1 |
Beachte: Wenn man -1,1 aufrundet, erhält man -1!

 Campus
Campus  Make Code
Make Code  Open Roberta Lab
Open Roberta Lab  Python
Python 